Bahay Blog~~Detalyadong Gabay sa Buong Adder~~

~~sa 2024/05/10~~ ~~627~~

Detalyadong Gabay sa Buong Adder

Sa lupain ng digital electronics at computer engineering, ang mga adders ay kumakatawan sa isa sa mga pinakamahalagang bloke ng gusali, pivotal sa konstruksyon at pag -andar ng mas masalimuot na mga circuit ng aritmetika.Bilang mga integral na sangkap ng aritmetic logic unit (ALU), pinadali ng mga adders ang maraming mga operasyon sa computing, mula sa pangunahing aritmetika hanggang sa kumplikadong mga lohikal na gawain na kinakailangan para sa mga operasyon ng system.Ang kanilang disenyo, na maaaring mag-iba mula sa mga simpleng half-adder hanggang sa mas kumplikadong buong adders, ay gumaganap ng isang mahalagang papel sa pagpapahusay ng kahusayan at bilis ng pagproseso sa loob ng mga digital system.Ang artikulong ito ay sumasalamin sa detalyadong arkitektura at functional nuances ng iba't ibang uri ng mga adders, na naglalarawan ng kanilang kritikal na papel sa modernong teknolohiya ng computing at paggalugad ng kanilang pagpapatakbo ng lohika, circuitry, at mga aplikasyon sa loob ng mas malawak na konteksto ng disenyo ng digital na lohika.

Catalog

1. Ano ang isang adder?

2. Half Adder

3. Buong adder

4. Buong talahanayan ng katotohanan ng adder

5. Mga Equation ng Katangian ng isang Buong Adder

6. Pagpapatupad ng isang buong adder circuit

7. Mga Bentahe at Kakulangan ng Buong Adders

8. Ang mga aplikasyon ng buong adders sa digital na lohika

9. Mga halimbawa ng buong pagpapatupad ng adder

10. Konklusyon

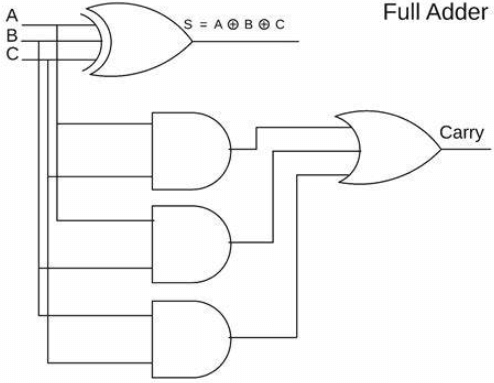
Larawan 1: buong adder

Ano ang isang adder?

Ang isang adder ay isang pangunahing sangkap sa electronic engineering at digital na disenyo ng lohika at gumaganap ng isang pangunahing papel sa mas kumplikadong mga computer system.Bilang isang bahagi ng yunit ng lohika ng aritmetika (ALU), ang adder ay humahawak ng iba't ibang mga mahahalagang gawain sa computing.Ang kahusayan at pagganap ng buong processor ay direktang naapektuhan ng disenyo at pag -andar ng adder.

Sa processor, ang adder ay ginagamit hindi lamang para sa mga pangunahing operasyon ng aritmetika tulad ng karagdagan at pagbabawas, ngunit nakikibahagi din ito sa isang mas malawak na hanay ng mga lohikal na operasyon.Halimbawa, kapag nagpapatakbo ng mga programa, ang processor ay madalas na kailangang makalkula ang mga bagong address ng memorya.Ito ay karaniwang ginagawa sa pamamagitan ng pagdaragdag sa o pagbabawas mula sa kasalukuyang address - isang gawain na isinasagawa ng adder.Kinokontrol nila ang bilang ng mga iterasyon ng loop at ang pangkalahatang daloy sa pamamagitan ng pagdaragdag at pag -decrement ng mga counter.Sa mas kumplikadong mga aplikasyon, tulad ng pag -index ng talahanayan, mabilis na hanapin ng mga adders ang data sa pamamagitan ng pagkalkula ng mga offset.Mahalaga ito para sa mga sistema ng pamamahala ng database, konstruksyon ng tagatala, at malakihang pagproseso ng data.Ang mga adders ay susi din sa pagpapatupad ng ilang mga diskarte sa pagmamapa sa mga multi-level cache system, gamit ang mga operasyon ng aritmetika upang matukoy ang posisyon ng data sa cache, sa gayon na-optimize ang kahusayan sa pag-access.

Teknolohiya, ang mga adders ay ipinatupad sa pamamagitan ng iba't ibang mga disenyo ng circuit kabilang ang kahanay, serial, at pipeline adders.Ang mga paralel na adders ay pinapaboran para sa kanilang kakayahang hawakan ang maraming mga numero nang sabay -sabay, na ginagawang angkop para sa mga senaryo na nangangailangan ng mabilis na pagkalkula.Ang mga serial adders, sa kabilang banda, ay mag-proseso ng isang bit bawat cycle ng orasan at mainam para sa mga limitadong mapagkukunan o mababang lakas na kapaligiran.Ang mga adders ng pipeline ay naghahati sa proseso ng karagdagan sa ilang mga yugto, ang bawat paghawak ng isang bahagi ng operasyon ng karagdagan.Ang disenyo na ito ay makabuluhang pinalalaki ang bilis ng pagkalkula, lalo na sa mga kapaligiran sa computing ng mataas na pagganap.

Half Adder

Ang isang half-adder circuit ay isang pangunahing bloke ng gusali sa digital electronics, partikular na idinisenyo upang magdagdag ng dalawang solong binary digit.Ang circuit na ito ay bumubuo ng pundasyon ng isang buong adder at susi sa pag -unawa sa mas kumplikadong mga disenyo ng logic circuit.Sa kalahating adder, mayroong dalawang pangunahing pag -input, na may label na A at B, na kumakatawan sa pagpapalaki at ayon sa pagkakabanggit.Ang pag -setup na ito ay nagbibigay -daan upang makalkula ang kabuuan at magdala ng output nang hindi nangangailangan ng isang pagdala ng input mula sa mga nakaraang kalkulasyon.

Ang core ng isang half-adder ay binubuo ng dalawang lohika na pintuan: isang XOR gate at isang at gate.Ang XOR Gate ay may pananagutan para sa pagbuo ng kabuuan ng output.Nagpapatakbo ito sa ilalim ng isang simpleng panuntunan kung saan naglalabas ito ng isang 1 kung isa lamang sa mga input nito ay 1;Kung hindi man, naglalabas ito ng isang 0. Ang at gate, sa kabilang banda, ay humahawak sa pagdala ng output.Gumagawa ito ng isang 1 lamang kapag ang parehong mga input nito ay 1, na nakahanay nang perpekto sa mga pangunahing kinakailangan ng karagdagan sa binary.

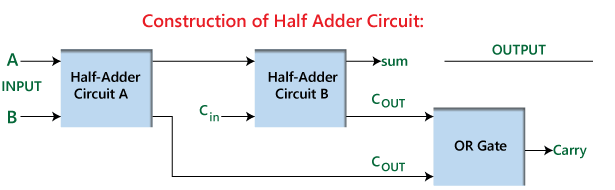
Larawan 2: Konstruksyon ng Half Adder

Ang mahusay at prangka na disenyo na ito ay nagbibigay -daan sa kalahating adder hindi lamang upang maisagawa ang pangunahing karagdagan sa binary nang nakapag -iisa kundi pati na rin maglingkod bilang isang bloke ng gusali para sa paglikha ng isang buong adder.Ang isang buong adder ay itinayo sa pamamagitan ng pagsasama ng dalawang kalahating adders na may karagdagang o gate.Sa pag -setup na ito, ang unang kalahating adder ay tumatagal sa paunang gawain ng karagdagan, na bumubuo ng isang paunang kabuuan at dalhin.Ang pangalawang kalahating adder pagkatapos ay pinoproseso ang dalhin mula sa una kasama ang isang karagdagang pag -input.Sa wakas, pinagsama ng o gate ang dalawa na nagdadala ng mga output upang makabuo ng pangwakas na pagdala ng output.Ang pag-aayos na ito ay nagpapaganda ng pag-andar ng adder, na nagpapagana upang mahawakan ang mas kumplikadong mga gawain ng karagdagan sa multi-bit, na nagpapakita ng malawakang aplikasyon at kahalagahan ng kalahating mga adders sa disenyo ng digital circuit.

Buong adder

Ang isang buong adder ay isang advanced na sangkap sa disenyo ng digital na lohika, na nilagyan upang hawakan ang pagdaragdag ng tatlong solong-bit na mga input ng binary, na karaniwang may label bilang A, B, at Carry-In (CIN).Pinapayagan ng disenyo na ito ang buong adder na mahusay na iproseso ang kumplikadong mga karagdagan sa binary sa pamamagitan ng pagsasama ng dalhin mula sa mga nakaraang mga kalkulasyon ng mas mababang-order sa isang solong operasyon.

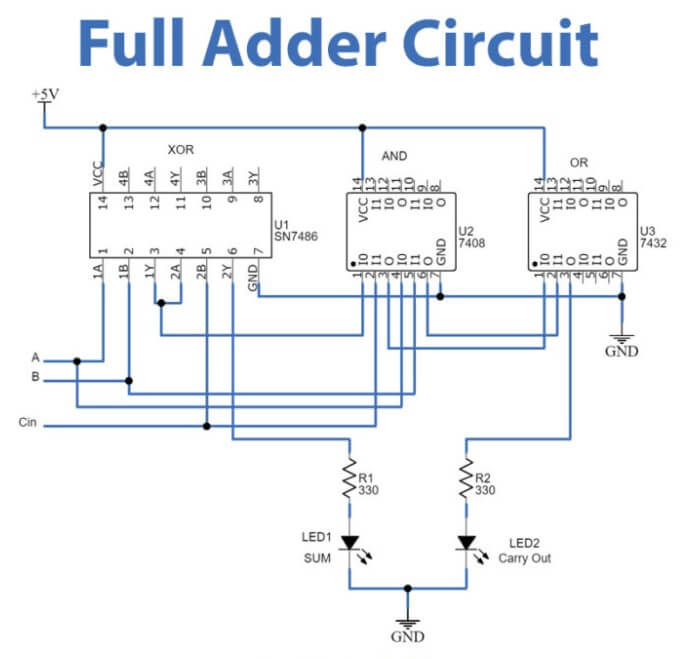
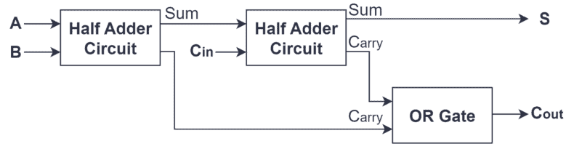
Larawan 3: Buong adder circuit

Functionally, ang isang buong adder ay maaaring mag-output ng isang dalawang-digit na kabuuan, na nangangahulugang ang output nito ay maaaring saklaw mula 0 hanggang 3, at maaari rin itong makagawa ng isang dala-dala (cout).Nangyayari ito dahil, kapag ang lahat ng mga input bits ay nakatakda sa 1 (a = 1, b = 1, cin = 1), ang kabuuan ng output ay magiging 1 (na kumakatawan sa binary 01), at ang isang pagdala ng 1 ay nabuo, na nagpapahiwatig naAng isang karagdagang dala ay kailangang maipasa sa susunod na mas mataas na bit.

Sa istruktura, ang buong adder sa pangkalahatan ay binubuo ng dalawang kalahating adders at isa o gate.Ang first-half adder ay tumatagal ng mga input A at B, na bumubuo ng isang paunang kabuuan at isang signal ng dala.Ang paunang kabuuan na ito ay pagkatapos ay pinakain, kasama ang dala-dala (CIN), sa ikalawang kalahating adder.Ang ikalawang kalahati ng papel ng adder ay upang idagdag ang halagang ito mula sa unang kalahating adder sa CIN, na gumagawa ng isa pang kabuuan at isang bagong pagdala ng output.Kasabay nito, ang pagdala ng output mula sa unang kalahati ng adder at ang pagdala ng output mula sa ikalawang kalahati ng adder ay pinagsama sa pamamagitan ng isang o gate, na nagtatapos sa pangwakas na pagdala (cout) ng buong adder.Ang disenyo ng istraktura na ito ay nagsisiguro na ang buong adder ay epektibong humahawak sa pagpapalaganap ng mga carrier bilang karagdagan sa mga operasyon, na ginagawang perpekto para sa pagpapatupad ng mga multi-bit na mga karagdagan sa binary.Kaya, ang disenyo ng buong adder ay hindi lamang nagpapabilis sa pagproseso ng data at nagpapahusay ng kahusayan ngunit pinasimple din ang pagiging kumplikado ng pagpapatupad ng hardware sa pamamagitan ng isang prangka na kumbinasyon ng mga logic gate, ginagawa itong isang kailangang-kailangan na sangkap sa multi-digit na karagdagan at ang aritmetika na logic unit (ALU).

Mga parameter	Half Adder	Buong adder
Paglalarawan	Ang Half Adder ay isang kombinasyon ng lohika Circuit na nagdaragdag ng dalawang 1-bit na numero.Ang half-adder ay gumagawa ng isang kabuuan ng dalawa Mga input.	Ang isang buong adder ay isang kombinasyon ng lohika circuit na nagsasagawa ng isang karagdagan na operasyon sa tatlong one-bit na mga numero ng binary. Ang buong adder ay gumagawa ng isang kabuuan ng tatlong mga input at may halaga.
Nakaraang dala	Ang nakaraang dala ay hindi ginagamit.	Ginagamit ang nakaraang dala.
Mga input	Sa kalahating adder, mayroong dalawang input bits (a, B).	Sa buong adder, mayroong tatlong mga input bits (A, b, c_sa).
Mga output	Ang nabuong output ay ng dalawang bits-sum at dalhin mula sa input ng 2 bits.	Ang nabuong output ay ng dalawang bits-sum at dalhin mula sa input ng 3 bits.
Ginamit bilang	Ang isang half-adder circuit ay hindi maaaring magamit sa Ang parehong paraan bilang isang full-adder circuit.	Ang isang buong adder circuit ay maaaring magamit sa lugar ng isang kalahating adder circuit.
Tampok	Ito ay simple at madaling ipatupad	Ang disenyo ng isang buong adder ay hindi tulad ng Simple bilang isang kalahating adder.
Lohikal na expression	Ang lohikal na expression para sa kalahating adder ay: S = a⊕b;C = a*b.	Ang lohikal na expression para sa buong adder ay: S = a⊕b⊕cin;C_Palabas= (ab)+(c_sa(a⊕b)).
Logic Gates	Binubuo ito ng isang ex-o gate at isa at Gate.	Binubuo ito ng dalawang ex-o, dalawa at pintuan, at isa o gate.
Mga Aplikasyon	Ginagamit ito sa mga calculator, computer, Mga aparato sa pagsukat ng digital, atbp.	Ginagamit ito sa maraming mga karagdagan karagdagan, digital processors, atbp.
Kahaliling pangalan	Walang kahaliling pangalan para sa kalahati Adder.	Ang isang buong adder ay kilala rin bilang isang ripple-carry Adder.

Tsart 1: Pagkakaiba sa pagitan ng kalahating adder at buong adder

Buong talahanayan ng katotohanan ng adder

Ang talahanayan ng katotohanan ng isang buong adder ay ang susi sa pag -unawa sa pagpapatakbo ng lohika, na detalyado ang tumpak na ugnayan sa pagitan ng mga kumbinasyon ng binary input at ang kanilang kaukulang mga output.Ipinapakita ng talahanayan na ito ang lahat ng mga potensyal na mga sitwasyon sa pag -input at ang kanilang mga kinalabasan, ginagawa itong isang mahalagang tool sa disenyo at pag -verify ng mga digital na circuit circuit.Ang buong adder ay nagpoproseso ng tatlong mga input: A, B, at isang dala-dala (CIN), ang bawat isa ay maaaring alinman sa 0 o 1. Nagreresulta ito sa walong posibleng mga kumbinasyon ng mga input.

Para sa bawat isa sa mga kumbinasyon na ito, ang mga output mula sa buong adder ay may kasamang kabuuan (kabuuan) at isang dala-dala (cout).Ang kabuuan ay ang modulo-2 karagdagan (XOR operation) ng tatlong mga input-a, b, at cin.Ang dala-dala ay nangyayari kung hindi bababa sa dalawa sa mga input bits ay 1. Sinasalamin nito ang buong kakayahan ng adder upang mahawakan ang dala-dala sa sunud-sunod na mga operasyon ng karagdagan, tinitiyak ang kawastuhan sa mga kalkulasyon na mas mataas.

Upang mailarawan, isaalang-alang ang senaryo ng pag-input kung saan ang lahat ng mga input ay 0 (A = 0, B = 0, C-in = 0).Ang output sum ay 0, at ang dalhin ay magiging 0 din, na nagpapahiwatig na walang karagdagang kabuuan o dalhin upang pamahalaan.Kung ang isang input bit lamang ay 1, tulad ng A = 1, B = 0, C-in = 0, ang output sum ay magiging 1 na walang dala, na nagpapakita na hindi na kailangang ilipat ang isang dala nang mas mataas.Kapag ang dalawang input bitout ay 1, na nagpapahiwatig ng isang dala na kailangang maipasa sa susunod na mas mataas na bit.Ang pinaka-kumplikadong senaryo ay nangyayari kapag ang lahat ng tatlong mga input bits ay 1 (a = 1, b = 1, c-in = 1);Ang output sum ay 1, at mayroong isang pagdadala ng 1, na nagmumungkahi na ang pamamahala ng pamamahala ay maaari ring kailanganin sa mas mataas na mga piraso.

A	B	C_sa	S	C_Palabas
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Tsart 2: Full Adder Truth Table

Mga Equation ng Katangian ng isang Buong Adder

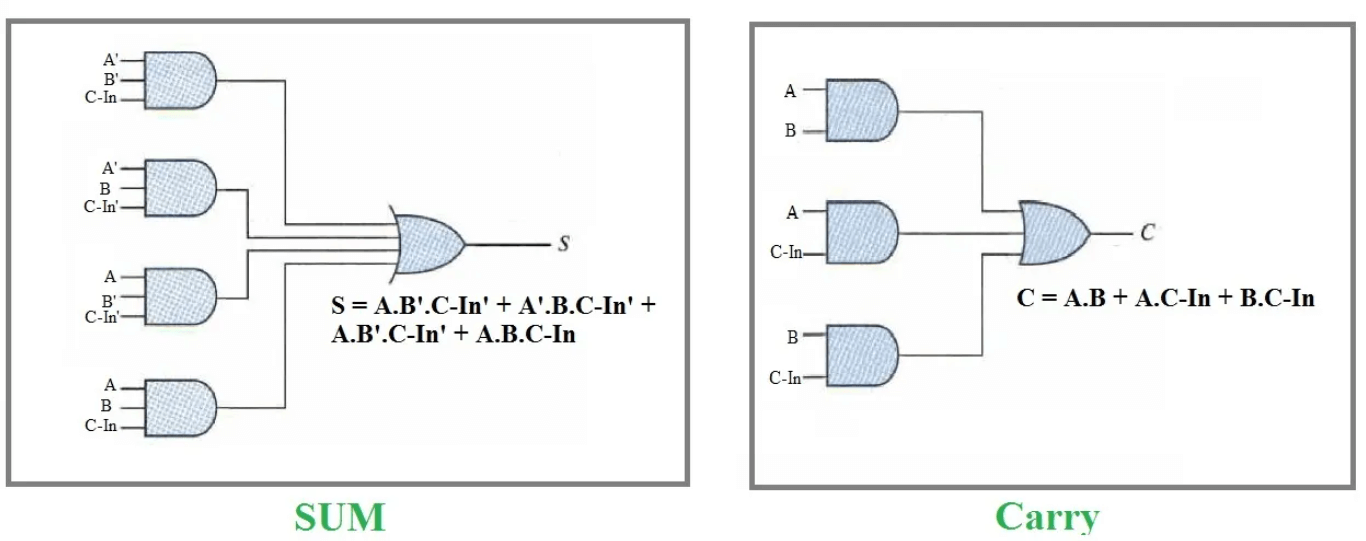
Ang pag-unawa sa buong adder ay nagsasangkot ng pag-iwas sa pag-andar nito gamit ang talahanayan ng katotohanan, kung saan ang iba't ibang mga kumbinasyon ng mga halaga ng pag-input A, B, at C-in ay humantong sa mga output ng kabuuan at cout.Upang maunawaan ang operasyon, pinasimple namin ang hakbang ng mga equation ng lohika.

Logic expression para sa kabuuan

Ang equation ay nagsisimula sa mga natatanging kaso kung saan ang kabuuan ay katumbas ng 1:

• A 'B' cin + a 'b cin' + a b 'cin' + ab cin

Ang equation na ito ay maaaring mai -condense sa pamamagitan ng pag -aayos ng mga termino at walang cin:

• cin (a 'b' + ab) + cin '(a' b + a b ')

Ang pagpapagaan na ito ay humahantong sa isang mas madaling form na ipatupad:

• cin xor (a xor b)

Ang representasyong ito ay nagpapakita na ang kabuuan ng output ay mahalagang operasyon ng XOR sa gitna ng A, B, at CIN, na kinukuha ang pangunahing pag -uugali ng karagdagan sa binary kung saan ang mga toggles batay sa isang kakaibang bilang ng mga.

Lohika para sa cout

Simula sa mga kondisyon kung saan nabuo ang dala:

• A 'B cin + a b' cin + ab c-in ' + ab cin

Pinapasimple ang equation, kinikilala namin ang mga termino na karaniwang nagsasangkot sa pagbuo ng isang dala:

• AB + B CIN + A CIN

Naghahanap para sa isa pang pamamaraan upang maipatupad ang cout, ang equation ay maaaring muling ayusin:

• AB + isang cin + b c-in (a + a ')

Ito ay nagpapalawak at recombines upang makuha ang lahat ng mga sitwasyon kung saan hindi bababa sa dalawang input ay 1:

• ab cin + ab + a c-in + a 'b cin

• ab (1 + cin) + a c-in + a 'b cin

• ab + a c-in (b + b ') + a' b cin

• ab + a b 'cin + a' b cin

• ab + cin (a 'b + a b')

Ang pangwakas na compact form para sa cout:

• AB + CIN (A XOR B)

Ang bersyon na ito ng dala-dalang equation ay nagpapakita kung paano ginawa ang cout alinman kapag ang parehong A at B ay 1, o kapag ang isa sa A o B ay 1 kasama ang isang dala-dala, sa gayon ay sumasaklaw sa lohika na kinakailangan upang pamahalaan ang pagdala ng pagpapalaganap sa multi-multi-Bit binary karagdagan.Ang naka -streamline na lohika na ito ay partikular na kapaki -pakinabang para sa pagpapatupad ng mahusay na mga digital circuit.

Larawan 4: Mga Equation ng isang buong adder

Pagpapatupad ng isang buong circuit ng adder

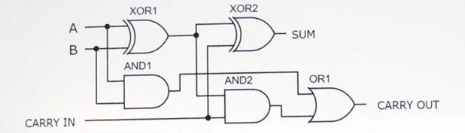
Ang pagpapatupad ng isang buong adder circuit ay nagsasangkot ng maingat na pag-iipon ng dalawang kalahating mga adders at isang o gate upang lumikha ng isang aparato na may kakayahang mahusay na paghawak sa pagdaragdag ng tatlong solong-bit na mga input ng binary.Ang pag -aayos na ito ay nag -optimize ng pagiging kumplikado ng circuit at tinitiyak ang parehong mahusay at tumpak na pagkalkula.

Upang magsimula, ang unang kalahati ng adder ay tumatagal ng dalawang pangunahing binary input, A at B, na siyang pangunahing numero na idaragdag.Ang pangunahing gawain nito ay upang makalkula ang kabuuan at ang paunang pagdala ng dalawang numero na ito.Dito, ang unang kalahating adder ay naghahatid ng dalawang kinalabasan: isang paunang kabuuan (sum1) at isang paunang pagdala (Carry1).Ang SUM1 ay nagmula sa operasyon ng XOR ng A at B, na nagpapahiwatig kung ang kabuuan ay may kakaibang bilang ng 1's.Carry1, ang resulta ng at operasyon sa pagitan ng A at B, ay nagpapahiwatig kung ang parehong mga numero ay 1, na nangangailangan ng isang dala sa susunod na mas mataas na bit.

Susunod, ang pangalawang kalahating adder ay sumali sa proseso.Ginagamit nito ang kabuuan ng output sum1 at ang pangatlong input cin (carry-in mula sa isang nakaraang pagkalkula) bilang mga input nito.Ang ikalawang kalahati ng adder ay gumagawa ng dalawang output: ang pangwakas na resulta ng kabuuan (SUM2) at ang pangalawang dala (Carry2).Ang SUM2, na kung saan ay ang resulta ng XOR ng SUM1 at CIN, ay kumakatawan sa pangwakas na kabuuan ng tatlong mga input, na nagpapakita ng pinagsama -samang karagdagan sa binary.Carry2, umuusbong mula sa at operasyon sa pagitan ng SUM1 at CIN, ay nagpapahiwatig ng isang dala na nabuo ng mga sangkap na ito.

Full Adder Circuit with Using Two Half Adder

Larawan 5: Buong adder circuit na may paggamit ng dalawang kalahating adder

Sa wakas, upang makumpleto ang disenyo ng buong adder, ang isang o gate ay kinakailangan upang hawakan ang dala ng mga output na Carry1 at Carry2 mula sa parehong kalahating adders.Tinitiyak ng ito o gate na ang anumang dala na nabuo sa panahon ng pagkalkula ay wastong maipasa sa panghuling output.Samakatuwid, ang Full Adder's Final Carry Output (Cout) ay ang o resulta ng Carry1 at Carry2.Ang pagsasama nito o gate ay ginagarantiyahan na ang lahat ng mga potensyal na dala ay tumpak na kinakalkula at ipinadala sa susunod na antas sa mga operasyon ng multi-bit na karagdagan, tinitiyak ang integridad ng operasyon ng aritmetika sa maraming mga piraso.

Mga kalamangan at mga hamon ng buong mga adders sa digital na lohika

Ang buong mga adders ay naglalaro ng isang kailangang -kailangan na papel sa disenyo ng digital na lohika, na nag -aalok ng maraming mga benepisyo na ginagawang mahalaga sa kanila sa iba't ibang mga senaryo sa pagproseso ng data at data.Ang kanilang pangunahing bentahe ay may kasamang kapansin -pansin na kakayahang umangkop, mabilis na bilis ng pagproseso, at mahusay na pamamahala ng pagdala.Ang mga katangiang ito ay ginagawang perpekto ang mga adders para sa pagpapatupad ng kumplikadong mga operasyon ng aritmetika at mga pag-andar ng lohika, lalo na sa mga aplikasyon na nangangailangan ng sunud-sunod na pagdaragdag ng multi-bit.

Kalamangan

Flexibility: Ang buong mga adders ay higit sa kanilang kakayahang iproseso ang maraming mga binary input (A, B, at CIN) nang sabay -sabay.Maaari rin silang mapalawak sa mas malaking adder arrays upang mahawakan ang mas mahabang mga numero ng binary.Mahalaga ang scalability na ito para sa pagbuo ng mataas na pagganap na mga yunit ng lohika ng aritmetika (ALU), na dapat magsagawa ng masalimuot na multi-bit na aritmetika at logic na operasyon.

Bilis: Salamat sa kanilang panloob na arkitektura ng pagproseso ng paralel, maaaring makumpleto ng buong adders ang pagdaragdag ng lahat ng mga input sa isang solong pag -ikot ng orasan habang tinutukoy din na magdala ng mga output.Ang kakayahang ito ay sumusuporta sa patuloy na pagdaragdag ng mga operasyon at kailangang-kailangan para sa pagproseso ng data ng real-time sa mga modernong microprocessors at mga aparato ng high-speed computing.

Mga Kakulangan

Gayunpaman, ang buong mga adders ay nagpapakita rin ng mga kapansin -pansin na kawalan:

Ang pagiging kumplikado sa disenyo at pagpapatupad: Ang buong mga adders ay nagsasangkot ng maraming mga logic gate at multi-level na pagdala ng pagpapalaganap, na ginagawang kumplikado ang kanilang disenyo.Ang pagiging kumplikado na ito ay hindi lamang nagdaragdag ng mga gastos sa pagmamanupaktura ngunit maaari ring makaapekto sa pagiging maaasahan ng mga circuit.

Mga isyu sa pagkaantala sa pagpapalaganap: Magdala ng pagpapalaganap ay maaaring dumaan sa maraming mga gate ng lohika, bawat isa ay nagdaragdag ng pagkaantala nito.Maaari itong limitahan ang pangkalahatang bilis ng computational sa panahon ng malakihang operasyon, lalo na sa malawak na mga computer system at sa disenyo ng napaka-malaking sukat na pagsasama (VLSI) at mga high-speed processors.Ang pagkaantala ay maaaring maging isang makabuluhang bottleneck sa pagganap.

Upang mabawasan ang mga isyung ito, ang mga inhinyero ay patuloy na galugarin ang mas mahusay na mga disenyo ng circuit.Kasama sa mga estratehiya ang paggamit ng mas mabilis na mga teknolohiya ng lohika ng gate, pag-optimize ng mga layout ng circuit upang paikliin ang mga haba ng landas, at pagbuo ng mga advanced na teknolohiya tulad ng mga nagdadagdag sa pag-save upang mabawasan ang mga pagkaantala sa pagdala ng pagpapalaganap.

Ang mga aplikasyon ng buong adders sa digital na lohika

Ang buong mga adders ay malawak na ginagamit sa digital na lohika, na pinapahalagahan para sa kanilang kakayahang umangkop at kahusayan, na ginagawang sentro ang mga ito sa maraming mga gawain sa pagproseso ng data at data.Ang kanilang application ay sumasaklaw mula sa pangunahing operasyon ng aritmetika sa kumplikadong pagproseso ng signal at control ng system.Narito ang isang detalyadong pagtingin sa ilang mga pangunahing lugar kung saan ang buong mga adders ay integral.

Arithmetic Circuits

Ang isa sa mga pinaka -prangka na paggamit ng buong adders ay sa mga aritmetika na circuit kung saan nagsasagawa sila ng karagdagan sa binary.Lalo na mahalaga sa karagdagan ng multi-bit na numero, ang buong mga adders ay namamahala ng mas mahabang mga pagkakasunud-sunod ng binary sa pamamagitan ng cascading.Sa pag -aayos na ito, ang bawat buong adder ay humahawak ng karagdagan para sa posisyon nito at ang dalhin mula sa mas mababang bit, pagkatapos ay ipasa ang bagong dala sa susunod na mas mataas na adder ng Bit.Pinapayagan ng kaskad na ito ang komprehensibong karagdagan ng multi-bit sa buong hanay ng mga numero.

Pagproseso ng data

Ang buong mga adders ay naglalaro din ng isang mahalagang papel sa mga advanced na gawain sa pagproseso ng data tulad ng Digital Signal Processing (DSP) para sa pag -filter at Fourier Transforms, kung saan kinakailangan ang tumpak at mabilis na operasyon ng aritmetika.Bilang karagdagan, sa kaharian ng seguridad ng impormasyon, kabilang ang data encryption at error detection at correction algorithm tulad ng mga tseke ng pagkakapare -pareho at cyclic redundancy check (CRC) code henerasyon, ang buong mga adders ay mahalaga para sa pagpapatupad ng mahahalagang operasyon.

Mga counter

Sa mga digital na counter, ang buong mga adders ay kailangang -kailangan para sa pagpapatupad ng parehong mga pag -andar ng pagdaragdag at pag -decrement, lalo na sa mga modular at kasabay na mga counter.Tumpak silang namamahala ng mga nagdadala at nanghihiram upang matiyak ang tumpak na pagbibilang.

Multiplexers (MUX) at Demultiplexers (Demux)

Sa mga multiplexer at demultiplexer, ang buong mga adders ay naglalaro ng isang kritikal na papel sa pagpili ng channel at pamamahagi ng data.Nakikilahok sila sa lohika na tumutukoy kung aling mga channel ang ginagamit para sa pag -input ng data at output, na gumagawa ng mga pagpapasya batay sa mga signal ng control ng lohika.

Teknolohiya ng memorya

Sa pagtugon sa memorya, ang buong mga adders ay tumutulong na makabuo ng mga signal ng address para sa pabago -bagong pag -access sa mga lokasyon ng memorya.Mahalaga ito lalo na sa dynamic na random-access memory (DRAM) at iba pang mga sistema ng imbakan, kung saan sinusuportahan ng buong adders ang mga kumplikadong kalkulasyon ng address upang mapahusay ang kahusayan ng pag-access sa memorya.

Arithmetic Logic Units (ALU)

Sa wakas, bilang mga pangunahing sangkap ng mga yunit ng lohika ng aritmetika sa mga microprocessors at mga digital signal processors, ang buong adders ay mahalaga.Hinahawak ng ALU ang lahat ng mga operasyon ng aritmetika at lohika, na may buong mga adders na tinitiyak na ang data ay naproseso pareho nang mabilis at tumpak.

Mga halimbawa ng buong pagpapatupad ng adder

Ang buong mga adders ay maaaring itayo gamit ang iba't ibang mga gate at mga pagsasaayos ng lohika.Dito, ginalugad namin ang apat na magkakaibang pagpapatupad, na itinampok ang kanilang mga pag -setup at pagpapatakbo.

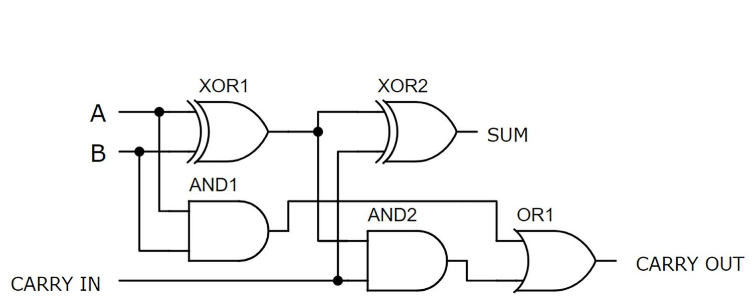
Buong adder na binuo gamit ang xor, at, at o mga pintuan

Full Adder Built with XOR, AND, and OR Logic Gates

Larawan 6: buong adder na binuo gamit ang xor, at, at o mga logic gate

Ang halimbawang ito ay nagpapakita ng isang buong adder na binuo sa isang breadboard gamit ang mga discrete transistors.Ang pagsasaayos ay binubuo ng limang mga gate ng lohika: dalawang xor gate, dalawa at pintuan, at isa o gate, na nangangailangan ng isang kabuuang 21 transistors.Ang mga input A at B ay konektado sa kaliwang kaliwa ng tinapay, na tumatanggap ng isang +5V supply.Ang mga input na ito ay kinokontrol gamit ang dalawang switch ng toggle.Dalawang LED sa kaliwang kaliwa ang nagpapahiwatig ng mga estado ng mga input A at B, habang ang dalawang LED sa kanang bahagi ay nagpapakita ng mga output.Ang mga resistors na ginamit sa circuit ay lahat ng 2.2k ohms.Kapag ang mga input A at B ay naka-on at ang dala-dala ay naka-off, ang output ay nagpapakita ng isang binary na halaga ng 10, na kumakatawan sa kabuuan 2 (1 + 1 + 0 = 10).Ang XOR Gates, na binuo kasama ang unang 12 transistors, ay humahawak sa pangunahing pagbubuod, habang ang mas mababang kalahati ng tinapay ay naglalaman ng at o o mga pintuan para sa mga operasyon, ang mga kable na naka-code na mga kable ay nagpapahusay ng kalinawan at pag-aayos.

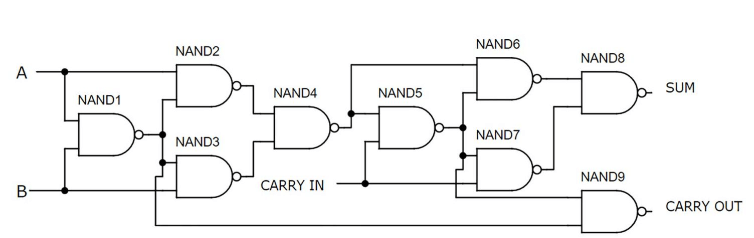
Buong adder gamit ang NAND Gates

Larawan 7: Buong adder gamit ang NAND Gates

Ang buong adder na ito ay gumagamit ng siyam na mga pintuan ng NAND, kasama ang bawat gate na ginawa mula sa dalawang transistor, na may kabuuang 18 transistors.Ang pamamaraang ito ay kabilang sa pinakasimpleng at pinaka -mahusay na mga paraan upang makabuo ng isang buong adder gamit ang mga discrete na sangkap.Ang lahat ng mga pintuan ay tipunin sa itaas na kalahati ng breadboard, habang ang mga switch ay sumasakop sa mas mababang kalahati.Ang pag-andar ng circuit ay ipinakita na may mga input a at b sa at ang pagdala, na nagreresulta sa isang output na halaga ng binary na 10, katumbas ng desimal 2.

Buong adder na may mga pintuan

Larawan 8: buong adder na may mga pintuan

Nakabuo na may siyam o pintuan, bawat isa ay nangangailangan ng dalawang transistor, ang setup na ito ay gumagamit din ng 18 transistors sa kabuuan.Ang pagtatayo ng isang buong adder kasama ang Nor Gates ay nag -aalok ng isang mahusay na alternatibo ngunit nagsasangkot ng mas kumplikadong mga kable kumpara sa NAND Gates.Ang bawat transistor sa NOR Gates ay nakabase, kasama ang mga kolektor na konektado ng mga orange jumper wires upang matiyak ang maayos at organisadong mga kable.Ang pagsasaayos na ito ay ipinapakita gamit ang mga input A at B na aktibo at ang dala-dala ay na-deactivate, na humahantong sa mga output kung saan aktibo ang dala at ang kabuuan ay naka-off.

Konklusyon

Sa buong paggalugad ng teknolohiyang Adder, mula sa mga pangunahing kalahating adders hanggang sa sopistikadong buong disenyo ng adder, maliwanag na ang mga sangkap na ito ay pundasyon sa pagsulong ng digital electronics.Ang mga katangian ng pagpapatakbo at mga halimbawa ng pagpapatupad ay nagbigay ng salungguhit sa kakayahang umangkop at kahusayan ng mga adders sa iba't ibang mga setting ng computational.Sa pamamagitan ng pagsusuri sa istraktura at pag -andar ng mga adders, lalo na sa pamamagitan ng kanilang mga talahanayan ng katotohanan at mga katangian ng katangian, nakakakuha tayo ng mahalagang pananaw sa kanilang mga kakayahan at hadlang.Ang kaalamang ito ay nakatulong sa pagsulong ng disenyo ng mas mahusay at mas mabilis na mga sistema ng computing.Sa huli, hindi lamang pinasimple ng mga adders ang kumplikadong mga kalkulasyon ng binary ngunit pinapagana din ang paglaganap ng teknolohiya sa mga lugar na magkakaibang bilang pagproseso ng data, paglalaan ng memorya, at pagproseso ng digital signal.Habang nagbabago ang digital na teknolohiya, ang patuloy na pagpipino at pagbabago sa disenyo ng adder ay magpapatuloy na maging isang pundasyon sa pagbuo ng mas advanced na mga arkitektura ng computational, na tinitiyak na ang mga pangunahing sangkap na ito ay mananatili sa gitna ng disenyo at pagpapatupad ng digital system.

Madalas na Itinanong [FAQ]

1. Ano ang isang buong adder circuit?

Ang isang buong adder ay isang digital circuit na nagdaragdag ng tatlong mga binary bits upang makabuo ng isang kabuuan at isang pagdala ng output.Ito ay dinisenyo upang hawakan ang pagdaragdag ng tatlong mga input: dalawang makabuluhang mga piraso at isang dala-dala mula sa isang nakaraang karagdagan.Pinapayagan nitong magamit ito sa sunud-sunod na mga yugto upang magdagdag ng mga multi-bit na mga numero ng binary.

2. Ilan at, o, xor sa buong adder?

Ang isang tipikal na buong adder ay naglalaman ng:

Dalawang xor gate para sa pagbuo ng kabuuan.

Dalawa at mga pintuan upang mag-ambag sa pagkalkula ng pagdala.

Isa o gate upang wakasan ang dala-out na output.

3. Ano ang dala ng input sa buong adder?

Ang Carry Input (CIN) sa isang buong adder ay ang dala ng bit mula sa pagdaragdag ng nakaraang mas mababang makabuluhang mga piraso sa multi-bit na karagdagan sa binary.Pinapayagan nito ang buong adder na isaalang-alang ang nakaraang dalhin kapag kinakalkula ang kasalukuyang kabuuan at ang bagong dala-dala.

4. Bakit gumamit ng isang buong adder sa halip na isang kalahating adder?

Ang isang buong adder ay ginagamit sa halip na isang kalahating adder dahil maaari itong magdagdag ng tatlong bits (kabilang ang dalhin mula sa mga nakaraang karagdagan), na ginagawang angkop para sa pag-chain nang magkasama upang magdagdag ng mga numero ng multi-bit.Ang isang half-adder ay maaari lamang magdagdag ng dalawang bits at walang probisyon para sa isang dala-dala, na nililimitahan ang paggamit nito sa pinakasimpleng anyo ng binary karagdagan nang walang sunud-sunod na pagpapalaganap.

Tungkol sa atin

ALLELCO LIMITED

Ang Allelco ay isang sikat na one-stop sa buong mundo Ang Procurement Service Distributor ng Hybrid Electronic Components, na nakatuon sa pagbibigay ng komprehensibong bahagi ng pagkuha at mga serbisyo ng supply chain para sa pandaigdigang industriya ng paggawa at pamamahagi, kabilang ang pandaigdigang nangungunang 500 pabrika ng OEM at mga independiyenteng broker.
Magbasa nang higit pa